Propriedades da radiciação
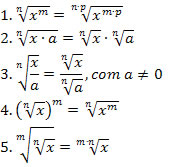
Exemplo 2. Simplifique a expressão
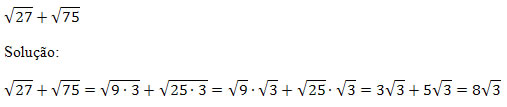
Exemplo 3. Verifique as propriedades da radiciação.
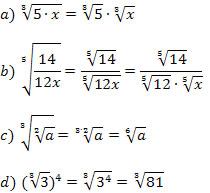
Exemplo 4. Obtenha a forma mais reduzida possível da expressão:
Solução: Podemos reescrever cada uma das raízes utilizando as propriedades da radiciação.

Racionalização de denominadores
Em alguns cálculos, você pode se deparar com raízes no denominador da fração. Para que você possa prosseguir com os cálculos, é conveniente que você elimine essas raízes do denominador - processo chamado de racionalização de denominadores. Isto é, transforma-se um denominador irracional em racional.
 o denominador
o denominador  é um número irracional e deve ser eliminado.
é um número irracional e deve ser eliminado.
Atenção: o importante é eliminar a raiz (que pode ser quadrada, cúbica, etc), mantendo uma fração "equivalente", ou seja, que representa o mesmo valor.
Uma dica é multiplicar tanto o numerador (parte de cima), quanto o denominador pelo mesmo número, o que não interfere na igualdade. Se a fração anterior for multiplicada em cima e em baixo por ficará:
ficará:
 . Note que
. Note que  é igual a 1, logo a multiplicação de um número por 1 não o altera.
é igual a 1, logo a multiplicação de um número por 1 não o altera.
Prosseguindo:
 o denominador
o denominador  é um número irracional e deve ser eliminado.
é um número irracional e deve ser eliminado.Atenção: o importante é eliminar a raiz (que pode ser quadrada, cúbica, etc), mantendo uma fração "equivalente", ou seja, que representa o mesmo valor.
Uma dica é multiplicar tanto o numerador (parte de cima), quanto o denominador pelo mesmo número, o que não interfere na igualdade. Se a fração anterior for multiplicada em cima e em baixo por
 ficará:
ficará: . Note que
. Note que  é igual a 1, logo a multiplicação de um número por 1 não o altera.
é igual a 1, logo a multiplicação de um número por 1 não o altera.Prosseguindo:
 |
Como se pode notar o denominador agora é um número racional (3).
Raízes não-quadradas
Para eliminar raízes cúbicas, ou de outros índices diferentes de 2 (lembre-se: raiz quadrada é, na verdade, uma raiz de índice 2!), é necessário utilizar um artifício.
 |
Multiplique, no numerador e no denominador, por uma raiz de mesmo radicando (o número dentro da raiz) e cujo índice seja equivalente ao índice da raiz original menos um. Por exemplo:
 |
Soma de raízes no denominador
Veja:
 |
Deve-se multiplicar por  .
.
Isso porque a multiplicação de por
por  é, na verdade, a multiplicação de (a + b). (a - b), um produto notável, cujo resultado é (a2 - b2) - isto é, os radicais somem!
é, na verdade, a multiplicação de (a + b). (a - b), um produto notável, cujo resultado é (a2 - b2) - isto é, os radicais somem!
 .
.Isso porque a multiplicação de
 por
por  é, na verdade, a multiplicação de (a + b). (a - b), um produto notável, cujo resultado é (a2 - b2) - isto é, os radicais somem!
é, na verdade, a multiplicação de (a + b). (a - b), um produto notável, cujo resultado é (a2 - b2) - isto é, os radicais somem! |
 |
Exemplo 1. Racionalize as seguintes frações:
Racionalizar a fração é fazer com que no denominador não exista uma raiz enésima de um número.
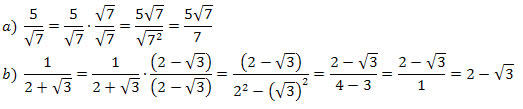
Exemplo 2. Racionalize as frações: